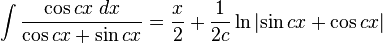TEMARIO DE CALCULO - 6.2 INTEGRALES TRIGONOMETRICAS

6.2 INTEGRALES TRIGONOMETRICA

Integrales que contienen solamente seno

$intsin cx;dx = -frac{1}{c}cos cx$

$intsin^n cx;dx = -frac{sin^{n-1} cxcos cx}{nc} + frac{n-1}{n}intsin^{n-2} cx;dx qquadmbox{(para }n>0mbox{)}$

$int xsin cx;dx = frac{sin cx}{c^2}-frac{xcos cx}{c}$

$int x^nsin cx;dx = -frac{x^n}{c}cos cx+frac{n}{c}int x^{n-1}cos cx;dx qquadmbox{(para }n>0mbox{)}$

$intfrac{sin cx}{x} dx = sum_{i=0}^infty (-1)^ifrac{(cx)^{2i+1}}{(2i+1)cdot (2i+1)!}$

$intfrac{sin cx}{x^n} dx = -frac{sin cx}{(n-1)x^{n-1}} + frac{c}{n-1}intfrac{cos cx}{x^{n-1}} dx$

$intfrac{dx}{sin cx} = frac{1}{c}lnleft|tanfrac{cx}{2}right|$

$intfrac{dx}{sin^n cx} = frac{cos cx}{c(n-1) sin^{n-1} cx}+frac{n-2}{n-1}intfrac{dx}{sin^{n-2}cx} qquadmbox{(para }n>1mbox{)}$

$intfrac{dx}{1pmsin cx} = frac{1}{c}tanleft(frac{cx}{2}mpfrac{pi}{4}right)$

$intfrac{x;dx}{1-sin cx} = frac{x}{c}cotleft(frac{pi}{4} - frac{cx}{2}right)+frac{2}{c^2}lnleft|sinleft(frac{pi}{4}-frac{cx}{2}right)right|$

$intfrac{sin cx;dx}{1pmsin cx} = pm x+frac{1}{c}tanleft(frac{pi}{4}mpfrac{cx}{2}right)$

$intsin c_1xsin c_2x;dx = frac{sin(c_1-c_2)x}{2(c_1-c_2)}-frac{sin(c_1+c_2)x}{2(c_1+c_2)} qquadmbox{(para }|c_1|neq|c_2|mbox{)}$

Integrales que contienen solamente cos

$intcos cx;dx = frac{1}{c}sin cx$

$intcos^n cx;dx = frac{cos^{n-1} cxsin cx}{nc} + frac{n-1}{n}intcos^{n-2} cx;dx qquadmbox{(para }n>0mbox{)}$

$int xcos cx;dx = -frac{cos cx}{c^2} + frac{xsin cx}{c}$

$int x^ncos cx;dx = frac{x^nsin cx}{c} - frac{n}{c}int x^{n-1}sin cx;dx$

$intfrac{cos cx}{x} dx = ln|cx|+sum_{i=1}^infty (-1)^ifrac{(cx)^{2i}}{2icdot(2i)!}$

$intfrac{cos cx}{x^n} dx = -frac{cos cx}{(n-1)x^{n-1}}-frac{c}{n-1}intfrac{sin cx}{x^{n-1}} dx qquadmbox{(para }nneq 1mbox{)}$

$intfrac{dx}{cos cx} = frac{1}{c}lnleft|tanleft(frac{cx}{2}+frac{pi}{4}right)right|$

$intfrac{dx}{cos^n cx} = frac{sin cx}{c(n-1) cos^{n-1} cx} + frac{n-2}{n-1}intfrac{dx}{cos^{n-2} cx} qquadmbox{(para }n>1mbox{)}$

$intfrac{dx}{1+cos cx} = frac{1}{c}tanfrac{cx}{2}$

$intfrac{dx}{1-cos cx} = -frac{1}{c}cotfrac{cx}{2}$

$intfrac{x;dx}{1+cos cx} = frac{x}{c}tan{cx}{2} + frac{2}{c^2}lnleft|cosfrac{cx}{2}right|$

$intfrac{x;dx}{1-cos cx} = -frac{x}{x}cot{cx}{2}+frac{2}{c^2}lnleft|sinfrac{cx}{2}right|$

$intfrac{cos cx;dx}{1+cos cx} = x - frac{1}{c}tanfrac{cx}{2}$

$intfrac{cos cx;dx}{1-cos cx} = -x-frac{1}{c}cotfrac{cx}{2}$

$intcos c_1xcos c_2x;dx = frac{sin(c_1-c_2)x}{2(c_1-c_2)}+frac{sin(c_1+c_2)x}{2(c_1+c_2)} qquadmbox{(para }|c_1|neq|c_2|mbox{)}$

Integrales que contienen solamente tan

$inttan cx;dx = -frac{1}{c}ln|cos cx|$

$inttan^n cx;dx = frac{1}{c(n-1)}tan^{n-1} cx-inttan^{n-2} cx;dx qquadmbox{(para }nneq 1mbox{)}$

$intfrac{dx}{tan cx + 1} = frac{x}{2} + frac{1}{2c}ln|sin cx + cos cx|$

$intfrac{dx}{tan cx - 1} = -frac{x}{2} + frac{1}{2c}ln|sin cx - cos cx|$

$intfrac{tan cx;dx}{tan cx + 1} = frac{x}{2} - frac{1}{2c}ln|sin cx + cos cx|$

$intfrac{tan cx;dx}{tan cx - 1} = frac{x}{2} + frac{1}{2c}ln|sin cx - cos cx|$

Rubi!

Integrales que contienen solamente cot

$intcot cx;dx = frac{1}{c}ln|sin cx|$

$intcot^n cx;dx = -frac{1}{c(n-1)}cot^{n-1} cx - intcot^{n-2} cx;dx qquadmbox{(para )}nneq 1mbox{)}$

$intfrac{dx}{1 + cot cx} = intfrac{tan cx;dx}{tan cx+1}$

$intfrac{dx}{1 - cot cx} = intfrac{tan cx;dx}{tan cx-1}$

Integrales que contienen sin y cos

$intfrac{dx}{cos cxpmsin cx} = frac{1}{csqrt{2}}lnleft|tanleft(frac{cx}{2}pmfrac{pi}{8}right)right|$

$intfrac{dx}{(cos cxpmsin cx)^2} = frac{1}{2c}tanleft(cxmpfrac{pi}{4}right)$

$intfrac{cos cx;dx}{cos cx + sin cx} = frac{x}{2} + frac{1}{2c}lnleft|sin cx + cos cxright|$

$intfrac{cos cx;dx}{cos cx - sin cx} = frac{x}{2} - frac{1}{2c}lnleft|sin cx - cos cxright|$

$intfrac{sin cx;dx}{cos cx + sin cx} = frac{x}{2} - frac{1}{2c}lnleft|sin cx + cos cxright|$

$intfrac{sin cx;dx}{cos cx - sin cx} = -frac{x}{2} - frac{1}{2c}lnleft|sin cx - cos cxright|$

$intfrac{cos cx;dx}{sin cx(1+cos cx)} = -frac{1}{4c}tan^2frac{cx}{2}+frac{1}{2c}lnleft|tanfrac{cx}{2}right|$

$intfrac{cos cx;dx}{sin cx(1+-cos cx)} = -frac{1}{4c}cot^2frac{cx}{2}-frac{1}{2c}lnleft|tanfrac{cx}{2}right|$

$intfrac{sin cx;dx}{cos cx(1+sin cx)} = frac{1}{4c}cot^2left(frac{cx}{2}+frac{pi}{4}right)+frac{1}{2c}lnleft|tanleft(frac{cx}{2}+frac{pi}{4}right)right|$

$intfrac{sin cx;dx}{cos cx(1-sin cx)} = frac{1}{4c}tan^2left(frac{cx}{2}+frac{pi}{4}right)-frac{1}{2c}lnleft|tanleft(frac{cx}{2}+frac{pi}{4}right)right|$

$intsin cxcos cx;dx = frac{1}{2c}sin^2 cx$

$intsin c_1xcos c_2x;dx = -frac{cos(c_1+c_2)x}{2(c_1+c_2)}-frac{cos(c_1-c_2)x}{2(c_1-c_2)} qquadmbox{(para }|c_1|neq|c_2|mbox{)}$

$intsin^n cxcos cx;dx = frac{1}{c(n+1)}sin^{n+1} cx qquadmbox{(para }nneq 1mbox{)}$

$intsin cxcos^n cx;dx = -frac{1}{c(n+1)}cos^{n+1} cx qquadmbox{(para }nneq 1mbox{)}$

$intsin^n cxcos^m cx;dx = -frac{sin^{n-1} cxcos^{m+1} cx}{c(n+m)}+frac{n-1}{n+m}intsin^{n-2} cxcos^m cx;dx qquadmbox{(para }m,n>0mbox{)}$

también: $intsin^n cxcos^m cx;dx = frac{sin^{n+1} cxcos^{m-1} cx}{c(n+m)} + frac{m-1}{n+m}intsin^n cxcos^{m-2} cx;dx qquadmbox{(para }m,n>0mbox{)}$

$intfrac{dx}{sin cxcos cx} = frac{1}{c}lnleft|tan cxright|$

$intfrac{dx}{sin cxcos^n cx} = frac{1}{c(n-1)cos^{n-1} cx}+intfrac{dx}{sin cxcos^{n-2} cx} qquadmbox{(para }nneq 1mbox{)}$

$intfrac{dx}{sin^n cxcos cx} = -frac{1}{c(n-1)sin^{n-1} cx}+intfrac{dx}{sin^{n-2} cxcos cx} qquadmbox{(para }nneq 1mbox{)}$

$intfrac{sin cx;dx}{cos^n cx} = frac{1}{c(n-1)cos^{n-1} cx} qquadmbox{(para }nneq 1mbox{)}$

$intfrac{sin^2 cx;dx}{cos cx} = -frac{1}{c}sin cx+frac{1}{c}lnleft|tanleft(frac{pi}{4}+frac{cx}{2}right)right|$

$intfrac{sin^2 cx;dx}{cos^n cx} = frac{sin cx}{c(n-1)cos^{n-1}cx}-frac{1}{n-1}intfrac{dx}{cos^{n-2}cx} qquadmbox{(para }nneq 1mbox{)}$

$intfrac{sin^n cx;dx}{cos cx} = -frac{sin^{n-1} cx}{c(n-1)} + intfrac{sin^{n-2} cx;dx}{cos cx} qquadmbox{(for }nneq 1mbox{)}$

$intfrac{sin^n cx;dx}{cos^m cx} = frac{sin^{n+1} cx}{c(m-1)cos^{m-1} cx}-frac{n-m+2}{m-1}intfrac{sin^n cx;dx}{cos^{m-2} cx} qquadmbox{(para }mneq 1mbox{)}$

también: $intfrac{sin^n cx;dx}{cos^m cx} = -frac{sin^{n-1} cx}{c(n-m)cos^{m-1} cx}+frac{n-1}{n-m}intfrac{sin^{n-2} cx;dx}{cos^m cx} qquadmbox{(para }mneq nmbox{)}$

también: $intfrac{sin^n cx;dx}{cos^m cx} = frac{sin^{n-1} cx}{c(m-1)cos^{m-1} cx}-frac{n-1}{n-1}intfrac{sin^{n-1} cx;dx}{cos^{m-2} cx} qquadmbox{(para }mneq 1mbox{)}$

$intfrac{cos cx;dx}{sin^n cx} = -frac{1}{c(n-1)sin^{n-1} cx} qquadmbox{(para }nneq 1mbox{)}$

$intfrac{cos^2 cx;dx}{sin cx} = frac{1}{c}left(cos cx+lnleft|tanfrac{cx}{2}right|right)$

$intfrac{cos^2 cx;dx}{sin^n cx} = -frac{1}{n-1}left(frac{cos cx}{csin^{n-1} cx)}+intfrac{dx}{sin^{n-2} cx}right) qquadmbox{(para }nneq 1mbox{)}$

$intfrac{cos^n cx;dx}{sin^m cx} = -frac{cos^{n+1} cx}{c(m-1)sin^{m-1} cx} - frac{n-m-2}{m-1}intfrac{cos^n cx;dx}{sin^{m-2} cx} qquadmbox{(para }mneq 1mbox{)}$

también: $intfrac{cos^n cx;dx}{sin^m cx} = frac{cos^{n-1} cx}{c(n-m)sin^{m-1} cx} + frac{n-1}{n-m}intfrac{cos^{n-2} cx;dx}{sin^m cx} qquadmbox{(para }mneq nmbox{)}$

también: $intfrac{cos^n cx;dx}{sin^m cx} = -frac{cos^{n-1} cx}{c(m-1)sin^{m-1} cx} - frac{n-1}{m-1}intfrac{cos^{n-2} cx;dx}{sin^{m-2} cx} qquadmbox{(para }mneq 1mbox{)}$

çüÁμνΞ=== Integrales que contienen sin y tan === $int sin cx tan cx;dx = frac{1}{c}(ln|sec cx + tan cx| - sin cx),!$

$intfrac{tan^n cx;dx}{sin^2 cx} = frac{1}{c(n-1)} tan^{n-1} (cx) qquadmbox{(para }nneq 1mbox{)},!$

Integrales que contienen cos y tan

$intfrac{tan^n cx;dx}{cos^2 cx} = frac{1}{c(n+1)}tan^{n+1} cx qquadmbox{(para }nneq 1mbox{)}$

Integrales que contienen sin y cot

$intfrac{cot^n cx;dx}{sin^2 cx} = frac{1}{c(n+1)}cot^{n+1} cx qquadmbox{(para }nneq 1mbox{)}$

Integrales que contienen cos y cot

$intfrac{cot^n cx;dx}{cos^2 cx} = frac{1}{c(1-n)}tan^{1-n} cx qquadmbox{(para }nneq 1mbox{)},!$

Integrales que contienen tan y cot

$int cot cx tan cx;dx = x$

Integral de la Sec

$intsec^2 u;du = tan u+c$

$intsec u;du = ln |sec u + tan u |+c$