TEMARIO DE CALCULO - 6.1 INTEGRACION POR PARTES

6.1 INTEGRACION POR PARTES

Método de integración por partes

El método de integración por partes es el que resulta de aplicar el siguiente teorema:

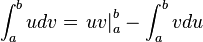$int_a^b u dv = left. uvright|_a^b - int_a^b vdu$ .

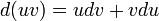
$d(uv) = u dv + v du$

$int_a^b d(u v) = int_a^b udv + int_a^b vdu$ .

Eligiendo adecuadamente los valores de 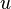$u$ y $dv$ , puede simplificarse mucho la resolución de la integral.

Para elegir la función $u$ se puede usar una de las siguiente reglas mnemotécnicas:

1) Arcoseno, arcocoseno..., Logarítmicas, Polinómicas, Exponenciales, Seno, coseno, tangente... ⇒ A L P E S.

   Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la palabra ALPES.

2) Logarítmicas, Inversas, Algebráicas, Trigonométricas, Exponenciales. ⇒ L I A T E.

   Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la palabra LIATE.

3) Inversas, Logarítmicas, Potenciales, Exponenciales, Trigonométricas ⇒ I L P E T

   Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la palabra ILPET